新規口座開設者限定のスタートアップ円定期預金、1年 年0.85%(税引前、2025.3.10までのキャンペーン金利)と好金利。
*3カ月 年1.20%(税引前)もあり さらに新規口座開設で1,500円、各種条件を満たすと最大31,000円がもらえます(要エントリー)。
今まで、バリュー経路(バリューパス)は単純に毎月1万円ずつ増えていくという前提で検証してきました。そこで、今回は、このバリュー経路を変えてみます。
例えば、年利回り5%で資産形成したいならば、バリュー経路も毎月の基準投資額に加え年5%ずつ複利的に増やしていくというのも一つの方法です。これにより、投資額、損益はおいといて、最終的には目標とした資産を形成することが出来ます。これも、バリュー平均法のメリットの一つでもあります。
今回の検証ですが、株価モデルは、単純に株価が上昇、下落する二つのケース、またバリュー平均法は、投資額、売却額に制限を加えない条件だけで見ていきます。
見出し
前提条件
- 毎月積立し、それを120カ月(10年間)継続する。
- ドルコスト法の毎月の積立額は1万円とする。
- バリュー平均法で、そのバリュー経路(パス)は投資開始月を1万円とし、その後、毎月の基準投資額1万円に加え、任意の月利で複利的に増加していくとする。
- バリュー平均法では、バリュー経路に従い、毎月、投資額を変更し、制限なく購入、売却を行う事とする。売却時の税金は考慮しない。
- 株価は投資開始月の価格を100円とする。
バリュー経路(バリューパス)
例えば、年利5%(-->月利換算0.41%)でバリュー経路が増えていく例で説明します。
1カ月目 10,000円
2カ月目 10,000 x (1 + 0.041) + 10,000 = 20,041円
3カ月目 20,041 x (1 + 0.041) + 10,000 = 30,122円
というふうに、バリュー経路を複利的に増加させていきます。
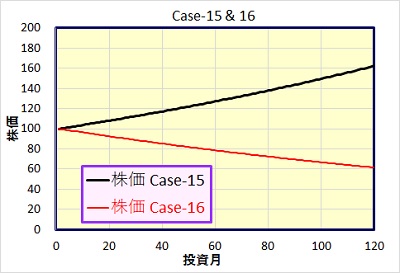
Case-15, 16 : 株価が単調に(複利的に)上昇、または下落していく場合。
株価が単調に上昇(Case-15)、下落(Case-16)していく場合です。
同じように単調に上昇、下落していくCase-1,2では、株価が毎月定額上昇(下落)していくモデルでしたが、今回のCase-15,16では、年利5%(月利0.41％)で複利的に上昇・下落するとします。バリュー経路も複利的に上昇させますので、その月利と比較する為です。
Case-15 ：株価が年利換算5%で複利的に上昇
バリュー平均法では、バリュー経路の増加率を年利換算0%, 2.5%, 5%, 7.5%,10%と5種類のケースで比較しています。
| ドル コスト | バリュー平均法 (バリュー経路の年利) | |||||
| 0% | 2.5% | 5.0% | 7.5% | 10% | ||
| 総投資額(千円) | 1,200 | 909 | 1,044 | 1,200 | 1,381 | 1,591 |
| 最終資産(千円) | 1,544 | 1,200 | 1,360 | 1,544 | 1,755 | 1,999 |
| 最終損益額(千円) | 344 | 291 | 316 | 344 | 374 | 408 |
| 年利回り | 4.92% | 4.93% | 4.93% | 4.92% | 4.92% | 4.91% |
| 平均購入株価 | 126.1 | 122.9 | 124.5 | 126.1 | 127.6 | 129.1 |
| 最大投資額(千円) | --- | 10 | 10 | 10 | 13 | 18 |
| 最小投資額(千円) | --- | 5 | 7 | 10 | 10 | 10 |
以前に説明したように(Case-1)、バリュー平均法は株価の単調な増加局面では、総投資額が抑えられ、結果的に損益(利益)がドルコスト法より少なくなってしまいます。
バリュー経路を複利的に増加させていくと、その年利が大きくなるにつれ、平均購入株価は上がっていきますが、損益(利益)は、どんどん増えていきます。株価の上昇率とバリュー経路の上昇率が一致した時(ともに5%)、ドルコスト法とバリュー平均法は同じ結果となり、株価上昇率以上にバリュー経路を増加させていくと、ドルコスト法以上の利益を上げることが出来ます。
これは簡単に予想できる結果ですね。
Case-16 ：株価が年利換算-5%で複利的に下落
今度は株価が下落していく場合です。
| ドル コスト | バリュー平均法 (バリュー経路の年利) | |||||
| 0% | 2.5% | 5.0% | 7.5% | 10% | ||
| 総投資額(千円) | 1,200 | 1,491 | 1,676 | 1,887 | 2,129 | 2,407 |
| 最終資産(千円) | 951 | 1,200 | 1,360 | 1,544 | 1,755 | 1,999 |
| 最終損益額(千円) | -249 | -291 | -316 | -344 | -374 | -408 |
| 年利回り | -4.70% | -4.69% | -4.69% | -4.68% | -4.68% | -4.68% |
| 平均購入株価 | 77.7 | 76.4 | 75.8 | 75.2 | 74.6 | 74.1 |
| 最大投資額(千円) | --- | 15 | 18 | 22 | 28 | 34 |
| 最小投資額(千円) | --- | 10 | 10 | 10 | 10 | 10 |
これもCase-2で説明しましたが、株価の単調な下落局面では、バリュー平均法は、その投資額を増やしていきますので、損失はどんどん膨らんでいきます。
バリュー経路の増加率(年利)を大きくしていくと、さらに、その損失は大きくなってしまいます。
勿論、このケースでも、バリュー経路を-5%とすれば、ドルコスト法と同じになるのですが、バリュー経路が基準投資額を積立てた場合より減っていくというのは、ちょっと考えにくいですね。
まとめ
今回は、バリュー経路を複利的に増やしていったらどうなるか、株価が単調に上昇・下落していく二つのケースで検証しました。
バリュー平均法が苦手とする株価の単調な増加、株価の上昇率以上にバリュー経路の上昇率を上げれば、ドルコスト法以上のパフォーマンスを上げることが出来ます。しかし、同じく苦手とする株価の単調な下落局面では、より大きな損失となってしまいます。
従って、バリュー経路の変更では、株価の単調な上昇・下落局面に弱いというバリュー平均法の欠点は解決できません。
今回は、ある程度予想された結果で、分かりやすかったかと思います。
さて、今まで、多くの株価モデルで検証してきましたが、これ以上やってもきりがないので、次回、今までの結果をまとめて、一旦、この検証は終わりとします。