下記記事で実際の先進国株式を例にとり、バリュー平均法で積立した結果から、ドルコスト法に対するメリット、デメリットをご紹介しました。
本記事では、実際の株価指数ではなく、簡単な株価モデルをいくつか想定し、それぞれのケースでドルコスト法とバリュー平均法との比較を行い、バリュー平均法に対する理解を深めていきたいと思います。
*2016.8.8 : 損益額の推移グラフを各ケースについて追加しました。
新規口座開設者限定のスタートアップ円定期預金、3カ月 年1.30%(税引前)、1年 年0.85%(税引前)と好金利。
さらに新規口座開設で1,500円、各種条件を満たすと最大20,000円がもらえます(要エントリー)。
見出し
前提条件
- 毎月積立し、それを120カ月(10年間)継続する。
- ドルコスト法の毎月の積立額は1万円とする。
- バリュー平均法で、そのバリュー経路(パス)は毎月1万円ずつ増加していくとする。
最終的な資産額は1万円 x 120カ月 = 120万円になる。 - バリュー平均法では、バリュー経路に従い、毎月、投資額を変更し、制限なく購入、売却を行う事とする。売却時の税金は考慮しない。
- 株価は投資開始月の価格を100円とする。
以下、各ケース毎に示す二つのグラフには、上側のグラフに株価(黒線)、ドルコスト法での毎月の投資額(赤線、当然1万円で一定です)、そしてバリュー平均法での投資額(グレー)をプロット、さらに下側のグラフに、株価とともに、損益額の推移をプロットしています。
尚、ドルコスト法をDCA、バリュー平均法をVAと略して表記する場合があります。
Case-1 : 単調に株価が上昇する場合
毎月、株価が0.5円ずつ上昇するモデルです。
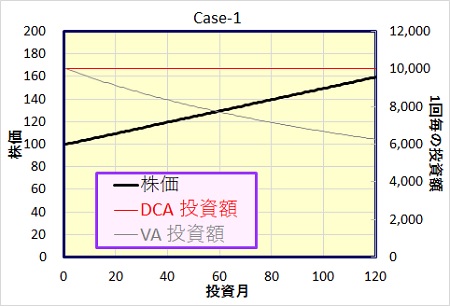

| ドルコスト | バリュー平均法 | VA-DCA(差分) | |
| 総投資額(千円) | 1,200 | 941 | -259 |
| 最終資産(千円) | 1,502 | 1,200 | -302 |
| 最終損益額(千円) | 302 | 259 | -43 |
| 年利回り | 4.40% | 4.43% | 0.03% |
| 平均購入株価 | 127.4 | 125.1 | -2.3 |
| 最大投資額(千円) | --- | 10 | --- |
| 最小投資額(千円) | --- | 6 | --- |
このケースでは、当然、利益が出るわけですが、年利回りはわずかにバリュー平均法が上回っているものの、損益額で見ると、ドルコスト法の方が大きく上回っています。
このようなケースでは、毎月積立額が減少していくバリュー平均法は、折角の利益を得るチャンスを逃している、機会損失をしているという事になります。
尚、表の下の行に、最大、最小投資額とありますが、これは毎月の投資額の最大、最小を示しています。値がマイナスの時は売却という事です。今回のケースでは最初の月の投資額が1万円で、その後、6千円程度まで単調に下がっています。
Case-2 : 単調に株価が下落する場合
毎月、株価が0.5円ずつ下落するモデルです。
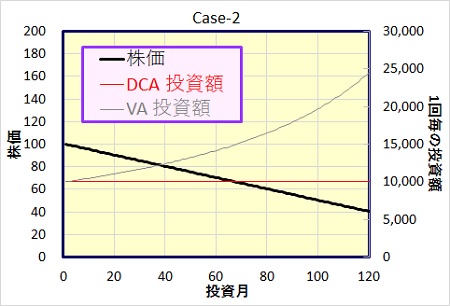
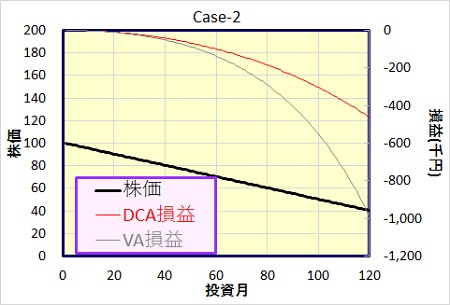
| ドルコスト | バリュー平均法 | VA-DCA(差分) | |
| 総投資額(千円) | 1,200 | 1,819 | 619 |
| 最終資産(千円) | 739 | 1,200 | 461 |
| 最終損益額(千円) | -461 | -619 | -159 |
| 年利回り | -9.98% | -10.19% | -0.21% |
| 平均購入株価 | 65.7 | 61.4 | -4.3 |
| 最大投資額(千円) | --- | 25 | --- |
| 最小投資額(千円) | --- | 10 | --- |
年利回りはわずかに、損益額は大きく、バリュー平均法が下回っています。
株価の下落とともに、投資額が増大していくバリュー平均法では、より大きな損失を出してしまいます。
ここまでのまとめ
株価が単調に上昇、下落していくケースでは、バリュー平均法では、上昇局面では機会損失、下落局面では損失の拡大と、全く良いところがありません。
Case-3 : 株価が上昇、下落を繰返す場合
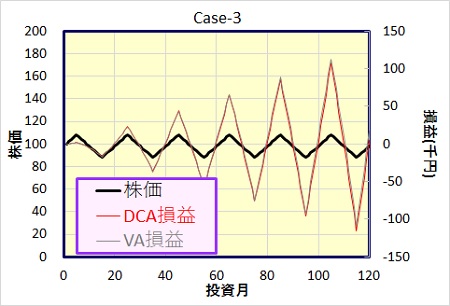
毎月、株価が10カ月毎に上昇、下落を繰り返すモデルです。一月の上昇、下落は2円、即ち、10カ月で20円上昇、次の10カ月で20円の下落を繰返す事としました。(最初と最後は5カ月)
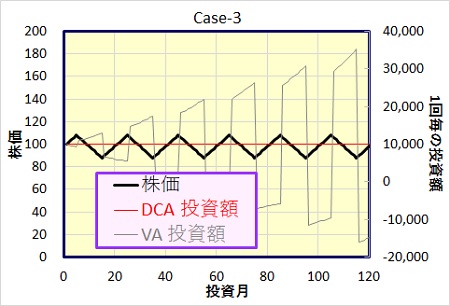
| ドルコスト | バリュー平均法 | VA-DCA(差分) | |
| 総投資額(千円) | 1,200 | 1,183 | -17 |
| 最終資産(千円) | 1,204 | 1,200 | -4 |
| 最終損益額(千円) | 4 | 17 | 13 |
| 年利回り | 0.07% | 0.28% | 0.21% |
| 平均購入株価 | 97.7 | 96.6 | -1.1 |
| 最大投資額(千円) | --- | 35 | --- |
| 最小投資額(千円) | --- | -16 | --- |
ようやく、バリュー平均法のメリットが見えてきました。損益額、年利回りとも上回っています。上昇、下落を繰返すパターンでバリュー平均法の効果がありそうです。
ただし、投資額の変動は、投資期間の後半になるほど大きくなり、最大で3.5万、最小で1.6万円の売却となっています。損益額も、株価の上下とともに、プラス、マイナスを繰返しています。
Case-3b : 株価が上昇、下落を繰返す場合 (より大きな変動)
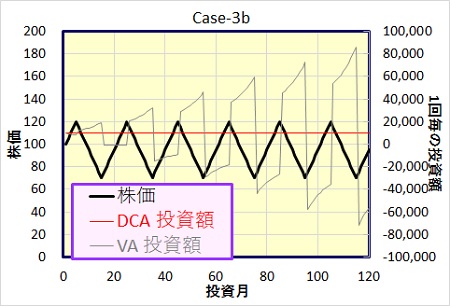
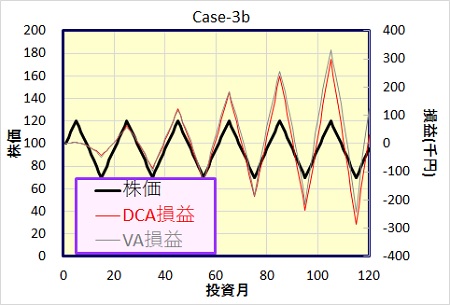
Case-3の上昇、下落の波をもっと大きくした場合です。一月の上昇、下落は5円、即ち、10カ月で50円上昇、次の10カ月で50円下落を繰返す事としましたが。Case-3より2.5倍変動幅が大きくなっています。
| ドルコスト | バリュー平均法 | VA-DCA(差分) | |
| 総投資額(千円) | 1,200 | 1,077 | -123 |
| 最終資産(千円) | 1,230 | 1,200 | -30 |
| 最終損益額(千円) | 30 | 123 | 94 |
| 年利回り | 0.48% | 1.99% | 1.51% |
| 平均購入株価 | 92.7 | 85.3 | -7.5 |
| 最大投資額(千円) | --- | 86 | --- |
| 最小投資額(千円) | --- | -72 | --- |
ドルコスト法、バリュー平均法ともに、Case-3より損益額、年利回りとも大幅に向上しています。バリュー平均法とドルコスト法の差分で見れば、より大きな上昇・下落の繰返しがある方がバリュー平均法の優位性が上がります。
損益額の推移もプラス・マイナスを繰返してはいますが、マイナス側でも、バリュー平均法の方が損失額が小さくなっています。
ただし、投資額・売却額の変動もより大きくなってしまいますが。
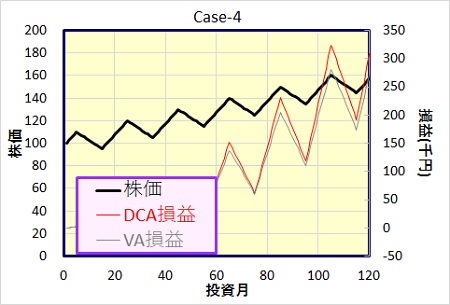
Case-4 : 株価が短期的には上昇、下落を繰返しながらも長いスパンで見れば上昇していく場合
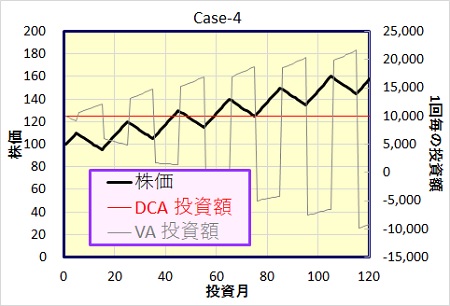
10カ月毎に上昇、下落を繰り返しながらも、長いスパンで見ると株価が上昇していくモデルです。Case-3のモデルに株価が毎月0.5円ずつ上昇していくファクターを追加しました。
| ドルコスト | バリュー平均法 | VA-DCA(差分) | |
| 総投資額(千円) | 1,200 | 929 | -271 |
| 最終資産(千円) | 1,509 | 1,200 | -309 |
| 最終損益額(千円) | 309 | 271 | -37 |
| 年利回り | 4.48% | 4.61% | 0.14% |
| 平均購入株価 | 125.3 | 121.9 | -3.4 |
| 最大投資額(千円) | --- | 22 | --- |
| 最小投資額(千円) | --- | -10 | --- |
このケースでは、年利回りはわずかにバリュー平均法が上回っていますが、損益額で見ると、ドルコスト法の方が大きくなっています。積立を重ねるごとにその差が大きくなっていることが下のグラフよりわかります。
Case-1(単調上昇)とCase-3(上昇、下落の繰返し)を合わせたケースになりますが、結局、上昇・下落の繰返しによるバリュー平均法のメリットより、単純な上昇局面でのバリュー平均法の機会損失というデメリットの方が勝った結果となっています。
勿論、上昇、下落の繰返しの波をもっと大きくし、長期的な上昇トレンドを緩やかにすれば、バリュー平均法のメリットが勝り、ドルコスト法より優位になります。
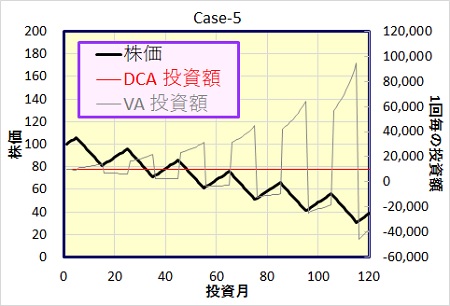
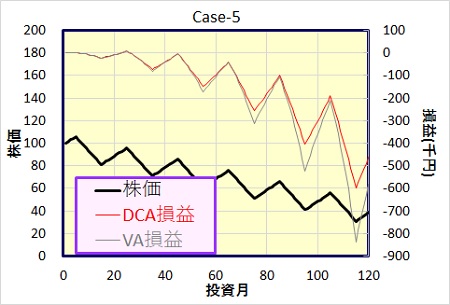
Case-5 : 株価が短期的には上昇、下落を繰返しながらも長いスパンで見れば下落していく場合
Case-4とは逆に長期的には下落していく場合です。Case-2と3を合わせたモデルです。
| ドルコスト | バリュー平均法 | VA-DCA(差分) | |
| 総投資額(千円) | 1,200 | 1,781 | 581 |
| 最終資産(千円) | 740 | 1,200 | 460 |
| 最終損益額(千円) | -460 | -581 | -121 |
| 年利回り | -9.97% | -9.29% | 0.67% |
| 平均購入株価 | 62.5 | 57.1 | -5.3 |
| 最大投資額(千円) | --- | 95 | --- |
| 最小投資額(千円) | --- | -46 | --- |
バリュー平均法、年利回りで若干上回るものの、損失額では大きくなってしまいます。積立を重ねるごとにその差が大きくなっていきます。
このケースでも、Case-4と同様、上昇、下落の繰返しの波をもっと大きくし、長期的な下降トレンドを緩やかにすれば、バリュー平均法のメリットが勝り、ドルコスト法より優位になります。
ここまでのまとめ
単調な上昇や下落局面では、そのメリットが見えなかったバリュー平均法ですが、株価が大きく上昇・下落を繰返す局面では、その変動幅が大きいほど、バリュー平均法が優位になる事がわかりました。
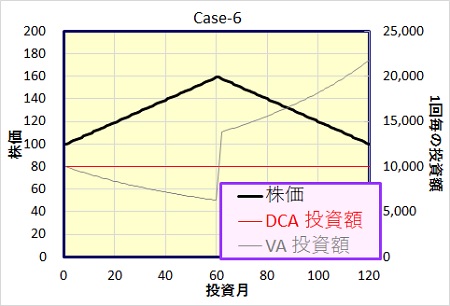
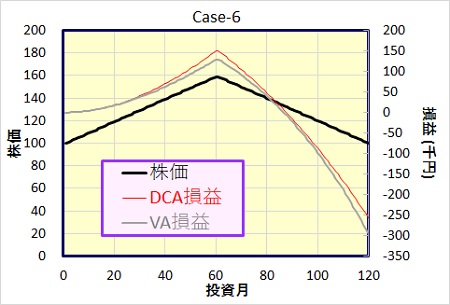
Case-6 : 株価が前半上昇、後半下落
株価は前半は単調に上昇し、後半は逆に下落、最後には積立開始時と同じ100円に戻るというモデルです。
| ドルコスト | バリュー平均法 | VA-DCA(差分) | |
| 総投資額(千円) | 1,200 | 1,497 | 297 |
| 最終資産(千円) | 944 | 1,200 | 256 |
| 最終損益額(千円) | -256 | -297 | -41 |
| 年利回り | -4.85% | -5.65% | -0.81% |
| 平均購入株価 | 127.1 | 124.8 | -2.4 |
| 最大投資額(千円) | --- | 22 | --- |
| 最小投資額(千円) | --- | 6 | --- |
前半の株価上昇局面で、投資額を減らしたバリュー平均法、その後の下落局面では(株価ピーク時の)保有口数が少ない分有利かと思っていましたが、結果はバリュー平均法の負け。下落局面での投資額が大きく増えてしまった為です。
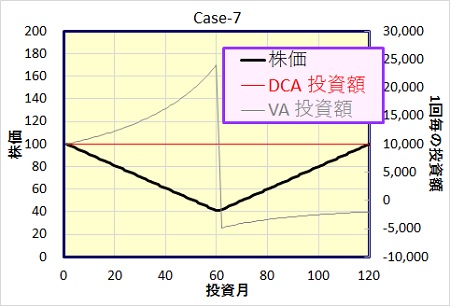
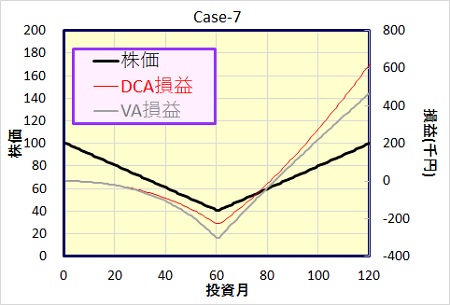
Case-7 : 株価が前半下落、後半上昇
Case-6の前半、後半を入替え、前半で単調に下落、後半で上昇というモデルです。
| ドルコスト | バリュー平均法 | VA-DCA(差分) | |
| 総投資額(千円) | 1,200 | 734 | -466 |
| 最終資産(千円) | 1,818 | 1,200 | -618 |
| 最終損益額(千円) | 618 | 466 | -151 |
| 年利回り | 8.05% | 6.25% | -1.80% |
| 平均購入株価 | 66.0 | 61.1 | -4.9 |
| 最大投資額(千円) | --- | 24 | --- |
| 最小投資額(千円) | --- | -5 | --- |
株価が安い時は、ドルコスト法より、さらに多く購入するのがバリュー平均法。ならば、下がってから上がるモデルではバリュー平均法が勝つだろうと予測していたのですが、これも結果はバリュー平均法の負け。
バリュー平均法は、株価が上昇局面に転じたとたん、投資額が大きく減ってしまうので、株価上昇の恩恵をあまり受けることが出来ないからです。
まとめ
ドルコスト法に対して、株価が安い時は、さらに多く購入し、株価が高い時は、購入額を大胆に減らすバリュー平均法。一見、素晴らしい方法で、万能のように思えますが、今回の結果を見ると、そう単純ではないようです。
株価の単調な上昇、下落に対しては、ドルコスト法に負けてしまいます。バリュー平均法が真価を発揮するのは、株価が大きく上昇・下落を繰返すような局面のみです。
ここで以前の記事で使った日経平均を10年間積立てた場合のドルコスト法とバリュー平均法の損益額を比較したグラフを再度お見せします。
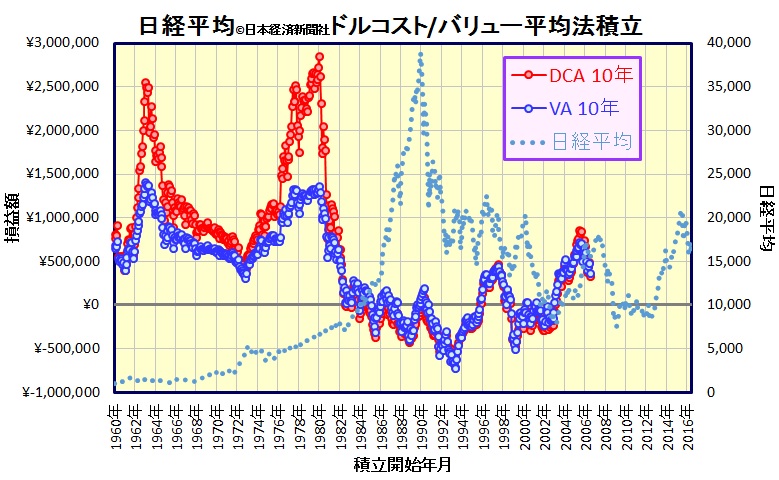
例えば、1980年に積立開始した場合、(青色でプロットした)バリュー平均法より、(赤色でプロットした)ドルコスト法の方が大きく上回っている事がわかります。1980年に積立て開始の場合、10年間の積立なので、1990年まで積立したという前提での損益額です。1980~90年の日経平均株価(破線でプロット)は、月々の変動が無視できるほど、株価は大きく上昇しています。
これは、「単調な上昇ではバリュー平均法よりドルコスト法の方が良いパフォーマンスを示す」という特徴を良く表している結果と言えるでしょう。
次回は、バリュー平均法の優位性が発揮されるであろう、もっと上昇・下落を多くしたモデルで検証し、さらに理解を深めていきたいと思っています。
*日経平均株価の指数に関する著作権ならびに「日経」および「指数」の表示に対する知的財産権、その他一切の権利はすべて日本経済新聞社に帰属しています。
